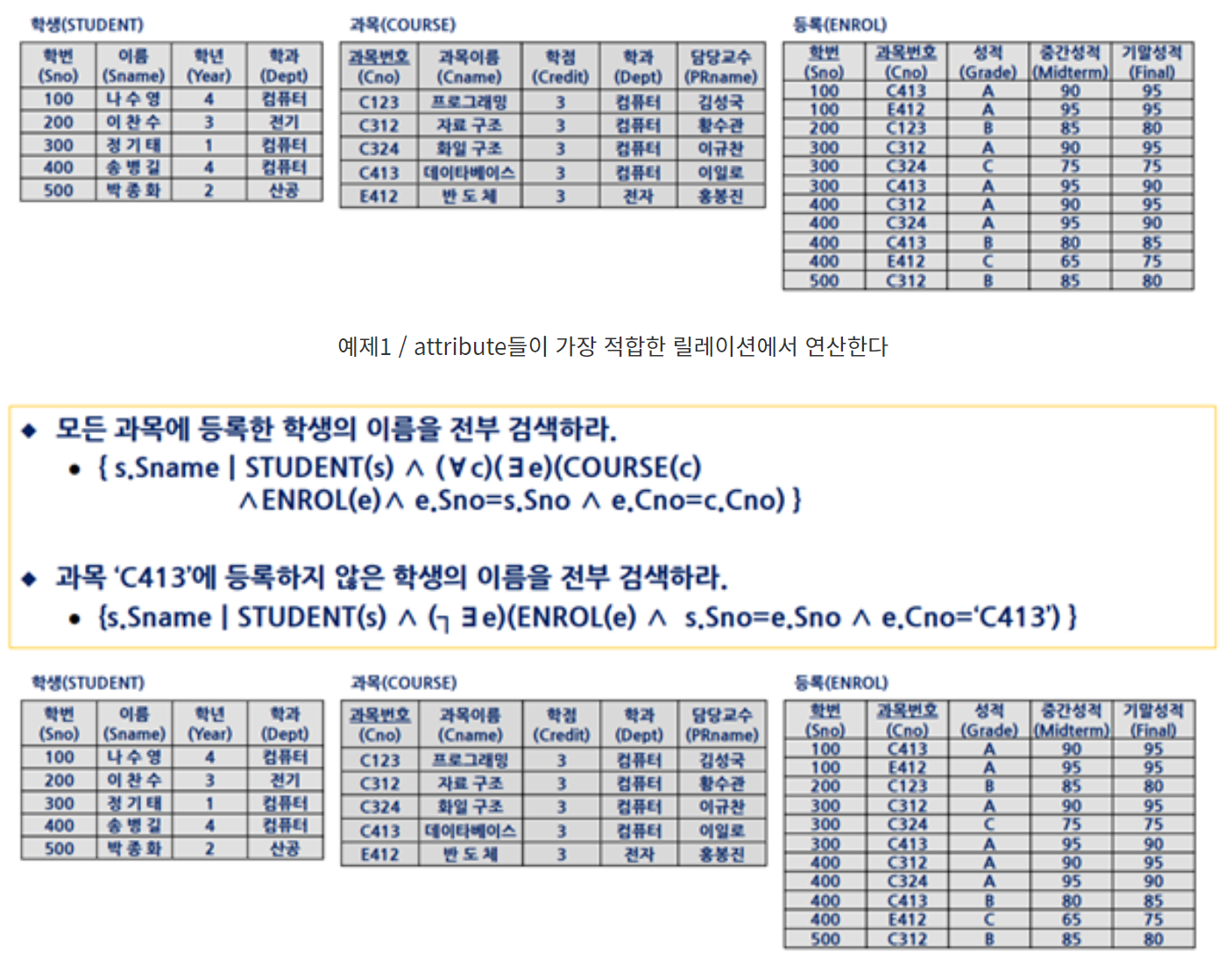
관계형 데이터 언어
관계 대수학
– 절차적 언어: 어떻게, 무엇
관계 해석
– 비절차적 언어: 무엇
– 튜플 관계 해석
– 도메인 관계 해석
@ 관계분석과 관계대수학은 표현과 기능이 동일하다.
관계 대수학
처리 관계를 위한 일련의 작업
관계 == 튜플 집합
이제 우리는 관계를 계산하기 위한 연산자를 소개할 것입니다.
Union: 두 관계를 하나의 관계로 결합합니다. 기호는 ∪, 일례는 R ∪ S이다. 예를 들어 R = {1, 2, 3}이고 S = {3, 4, 5}일 때 R ∪ S = {1, 2, 3, 4, 5}.
교집합: 두 관계가 공통적으로 갖는 튜플을 찾아 반환합니다. 기호는 ∩, 예를 들면 R ∩ S입니다. 예를 들어 R = {1, 2, 3}이고 S = {3, 4, 5}이면 R ∩ S = {3}입니다.
차이: 첫 번째 릴레이션에는 존재하지만 두 번째 릴레이션에는 없는 두 릴레이션에서 튜플을 반환합니다. 기호는 -, 예는 R – S입니다. 예를 들어 R = {1, 2, 3}이고 S = {3, 4, 5}이면 R – S = {1, 2}입니다.
데카르트 곱: 두 관계의 가능한 모든 조합을 찾아 단일 관계로 만듭니다. 기호는 x, 예를 들면 R x S이다. 2, a), (2, b)} 볼 수 없습니다.
선택: 조건에 맞는 튜플만 선택하여 반환합니다. 기호는 σ이며, 예를 들면 σA>5(R)입니다. 예를 들어, R = {(1, 2), (3, 4), (5, 6)}이면 σA>3(R) = {(5, 6)}입니다.
프로젝트: 지정된 속성만 선택하여 반환합니다. 기호는 π이고 예는 πA,B(R)입니다. 예를 들어, R = {(1, 2, 3), (4, 5, 6)}이면 πA,B(R) = {(1, 2), (4, 5)}입니다.
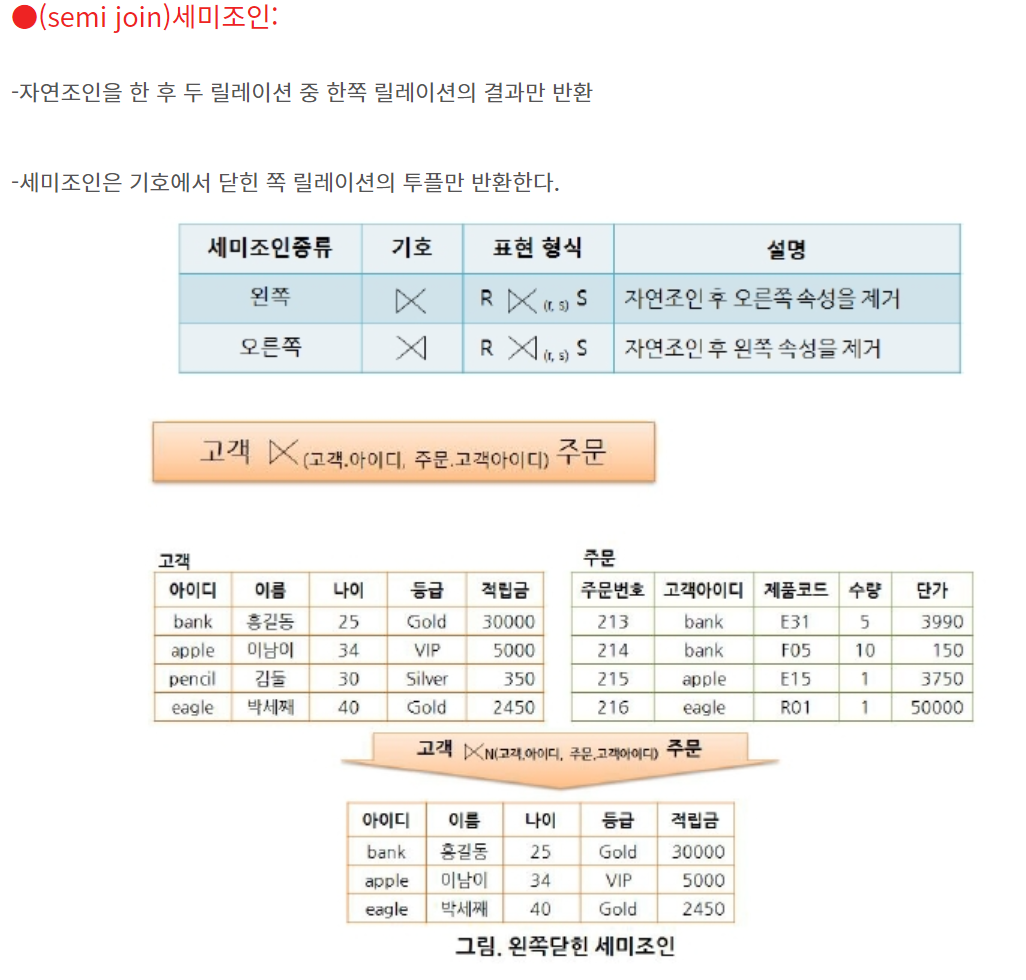
조인: 공통 속성을 기반으로 두 개의 관계를 하나의 관계로 결합합니다. 기호는 ⋈이고, 예는 R ⋈ S입니다. 조인이 중요하므로 나중에 더 많은 예를 다룰 것입니다.
나누기: 첫 번째 관계의 모든 조합이 두 번째 관계에 있는 경우에만 두 관계의 행을 반환합니다. 기호는 ÷, 예는 R ÷ S입니다.

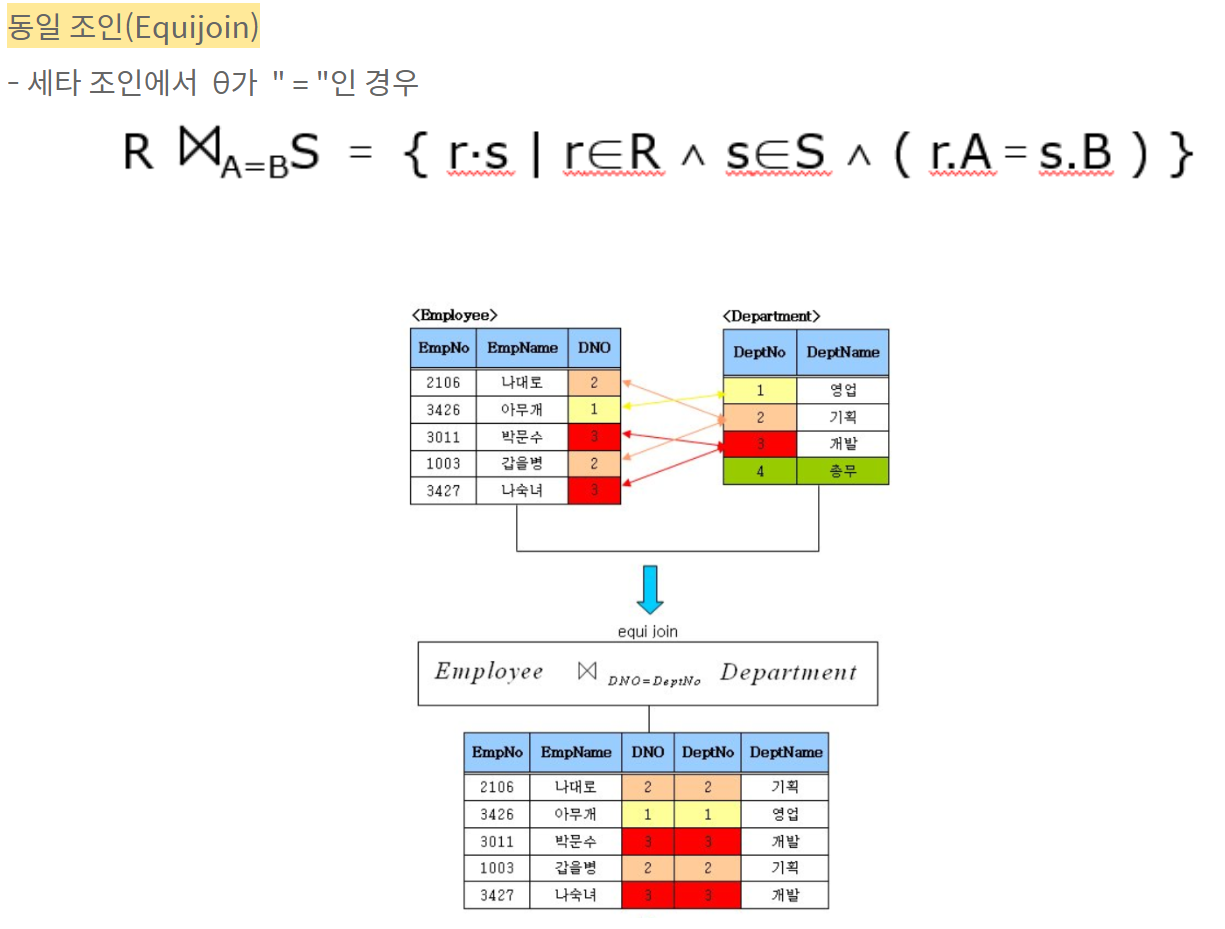
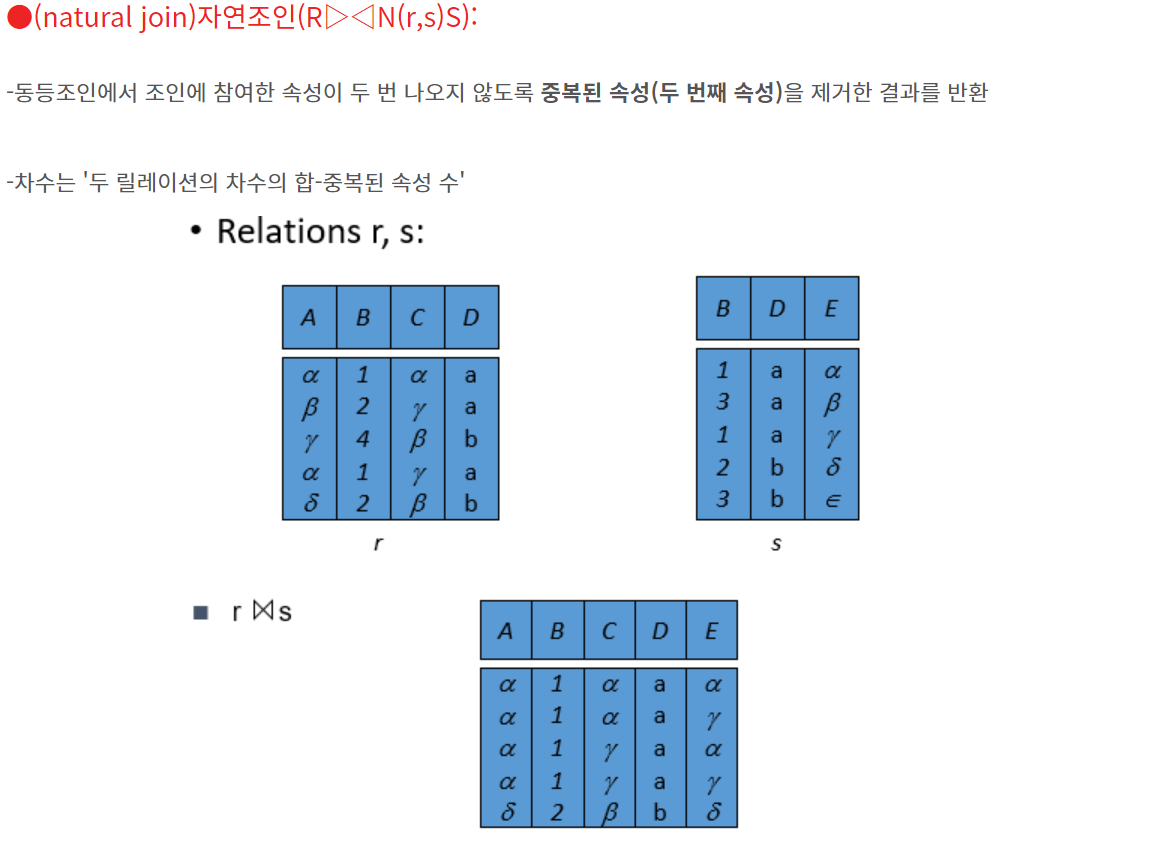
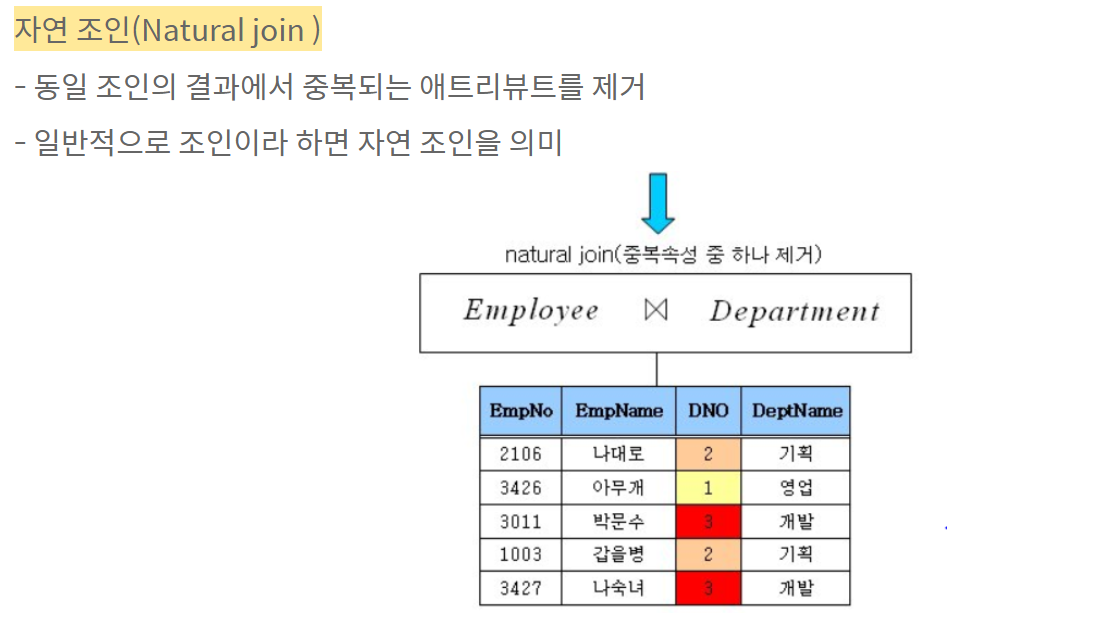
원천 : https://spidyweb.149
분할





대수적 표현이 가능해야 합니다.
튜플 관계의 해석